Area Enclosed by Two Curves

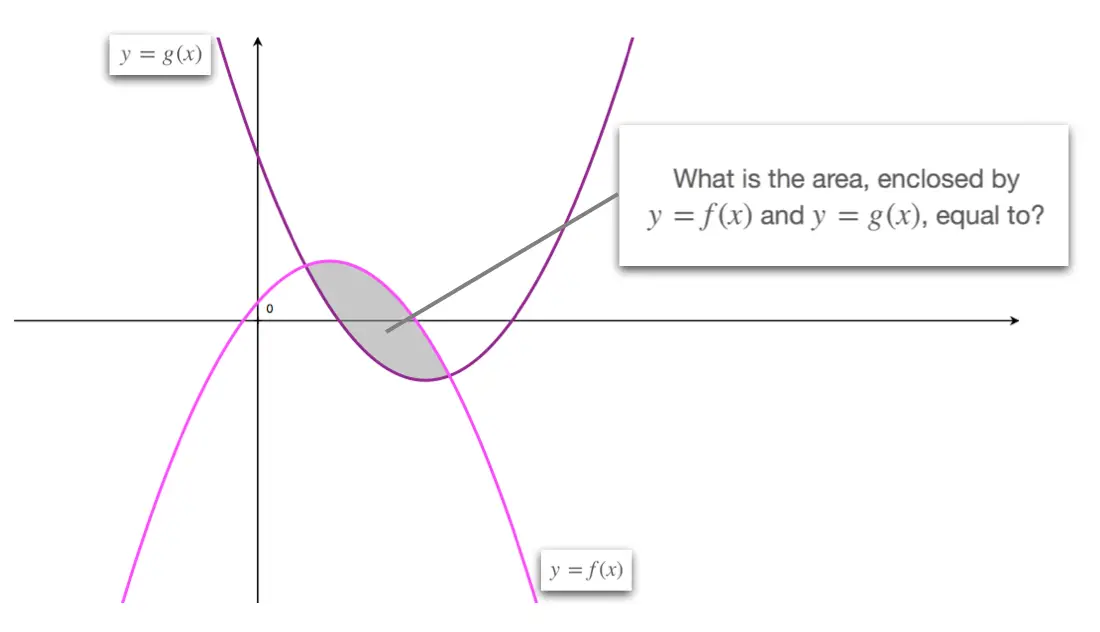
In this section we learn how to calculate the area enclosed between two curves, using definite integrals.

The typical type of scenario we'll be interested in is shown here. We'll often be required to calculate the area enclosed (or stuck between) two curve \(y = f(x)\) and \(y = g(x)\).

The method is explained in the following series of tutorials.

Tutorial 1: Method for Finding Area Enclosed Between 2 Curves

In this first tutorial we learn the method for finding the area enclosed between two curves using integration.

Formula - Area Enclosed Between Two Curves

Given two curves \(y=f(x)\) and \(y=g(x)\), which interesect at two points, with \(x\)-coordinates: \[x = a \quad \text \quad x = b\] such that \(f(x) \geq g(x)\), for \(a\leq x \leq b \), which means that \(y=f(x)\) is higher than (or above) \(y = g(x)\) over the interval \(a\leq x \leq b\).

The area enclosed by these two curves can be calculated using the formula: \[\text = \int_a^b \beginf(x)-g(x)\enddx\]

Tutorial 2: worked example

In this second tutorial we look at a worked example, in which we're given the coordinates of the points of intersection of the two curves. This should give us a good idea of how the formula "works".

The three-step method we've just seen is summarized here (make a note of it).

Step-by-Step Method

• Step 1: find the \(x\)-coordinates of the points of intersection of the two curves.
• Step 2: determine which of the two curves is above the other for \(a\leq x \leq b\). This can be done by calculating both \(f(x)\) and \(g(x)\)
• Step 3: use the enclosed area formula to calculae the area between the two curves: \[\text = \int_a^b \beginf(x)-g(x)\enddx\] Note: if in step 2 we find \(g(x)\geq f(x)\), for \(a\leq x \leq b\) then we use the formula: \[\text = \int_a^b \beging(x)-f(x)\enddx\]

Tutorial 3: worked example

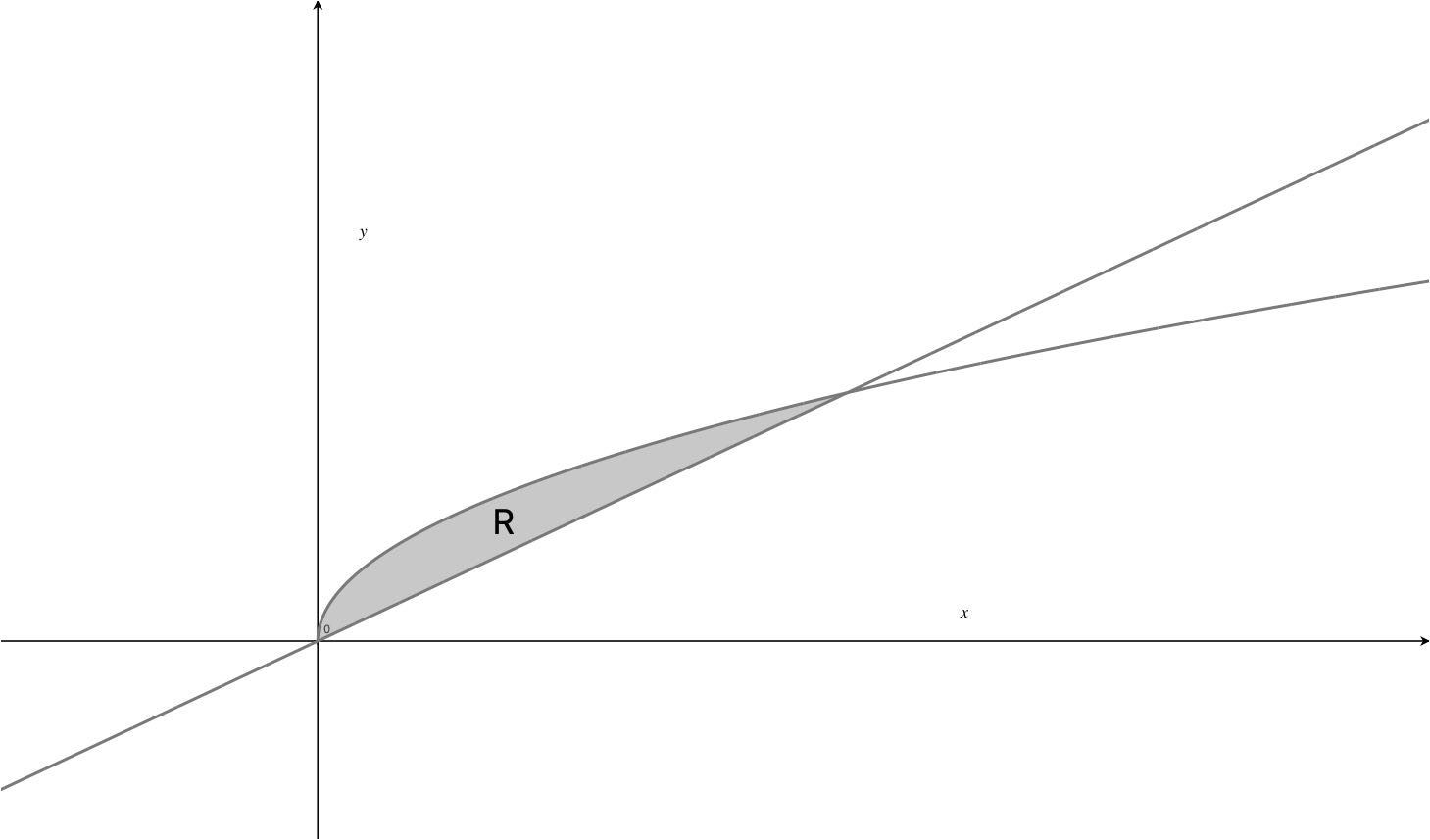
In this worked example we answer the following test-style question.

The region R is enclosed by: \[y= \sqrt \quad \text \quad y=x\] Find the exact value of R.

Using the three-step method, we saw above, try working through each of the following questions.

As good pratice, try solving each of these with and without using a graphical calculator.

Exercise 1

1. Find the area enclosed by the curves \(y = 2x^2+x-9\) and \(y = x-1\).
2. Find the area enclosed by the curves \(y = 3x^2 + 5x + 2\) and \(y=2x^2 + 7x + 2\).
3. Find the area enclosed by the curves \(y = 2x^2+ x - 1\) and \(y = x^2+3x+2\).
4. Find the area enclosed by the curves \(y = x^2-2x+1\) and \(y=x-1\).
5. Find the area enclosed by the curves \(y = -3x^2+5x+4\) and \(y = -x^2+3x-8\)

Answers Without Working

1. We find \(\text = \frac\approx 21.3\) units of area.
2. We find \(\text = \frac\approx 1.33\) units of area.
3. We find \(\text = \frac\approx 10.7\) units of area.
4. We find \(\text = \frac\approx 1.67\) units of area.
5. We find \(\text = \frac\approx 41.7\) units of area.

Answers with Working

Select the question number you'd like to see the working for: